Untersuchen sie Sinusfunktionen der Form ¦ (x) = a × sin(bx – c), wobei a,b,c feste reelle Zahlen sind.

1. Lassen sie zunächst einmal DERIVE die Sinusfunktion ¦ (x) = sin x zeichnen. Wählen sie dabei bei Grafik statt Beside diesmal Under und stellen sie den Trennwert auf die Zeile 5. Wählen sie als Maßstab bei x den Wert 3 und bei y den Wert 3.
2. Verändern sie nun zunächst den Wert a. Wählen sie a mit den Werten +2, +3, +5 und –1 (erste Funktion also ¦ (x) = 2 × sinx). Löschen sie die jeweils die Graphen wieder bis auf die Sinuskurve! Wie ändert sich der Graph?
   Notieren sie das Ergebnis in Form zweier Wenn-Dann-Sätze in ihren Unterlagen.
3. Löschen sie die Grafik bis auf die Sinuskurve. Stellen sie den y-Maßstab zurück auf 1.
   Nun soll a wieder gleich 1 sein. Verändern sie nun b, in dem sie für b die Werte +2, +3, +5 und –1 wählen (erste Funktion also ¦ (x) = sin(2x)). Löschen sie die jeweils die Graphen wieder bis auf die Sinuskurve! Wie ändert sich der Graph?
   Notieren sie das Ergebnis in Form zweier Wenn-Dann-Sätze in ihren Unterlagen.
   Vergleichen Sie die Ergebnisse von a=–1 und b=–1! Begründung?
4. Löschen sie die Grafik bis auf die Sinuskurve.
   Nun sollen a=1 und b=1 sein. Verändern sie nun c, in dem sie für c die Werte +1, +3, +5 und –2 wählen (erste Funktion also ¦ (x) = sin(x–1)). Löschen sie die jeweils die Graphen wieder bis auf die Sinuskurve! Wie ändert sich der Graph?
   Notieren sie das Ergebnis in Form zweier Wenn-Dann-Sätze in ihren Unterlagen.
5. Zeichnen sie – ohne DERIVE zu benutzen – den Graphen der Funktion

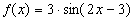
in ihre Unterlagen.

Zusammenfassung:

Der Graph der Sinusfunktion ¦ (x) = a × sin(bx–c) ist gegenüber dem Graphen der Sinuskurve

• um den Faktor a in y-Richtung ______________ (a heißt Amplitude);
• um c nach ________ _____________ (c heißt Phase);
• um den Faktor b in x-Richtung ______________. b bestimmt dabei, wo die volle Sinusperiode endet. Der Wert 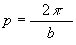heißt deshalb Periodenlänge.